9 minute read

이번 포스팅에서는 컨볼루션 레이어(Convolutional Layer)의 기본 개념과 수학적 표현, 연산 방식(스트라이드, 패딩, 채널 처리 등), 1D와 2D 컨볼루션의 차이점과 활용, 그리고 행렬-벡터 곱셈을 이용한 연산 최적화 방법까지 폭넓게 살펴보겠습니다.

CNN 시리즈

  1. Convolutional Neural Networks 개요
  2. CNN의 역사와 발전 과정, 주요 모델들
  3. 컨볼루션 레이어(Convolutional Layer)
  4. 패딩(Padding)과 스트라이드(Stride)
  5. 풀링 레이어(Pooling Layer)
  6. 정규화 레이어(Normalization Layer)

1. 컨볼루션 레이어(Convolutional Layer)란?

1.1. 정의

컨볼루션 레이어는 작은 크기의 필터(Kernel)를 입력 데이터 위에서 이동 적용하며, 필터와 겹치는 입력 영역 간의 원소별 곱을 합산(내적)하는 연산을 수행하는 신경망 층입니다. 이를 통해 이미지나 시계열 등의 Local Pattern을 효과적으로 추출할 수 있습니다.

  • 예: \(5 \times 5\) 입력에 \(3 \times 3\) 필터를 적용할 경우, 필터는 입력을 가로세로로 이동하며 매 위치마다 Convolution 결과를 계산하여 Feature map을 생성합니다.
  • 컨볼루션 레이어는 입력 전체에 완전 연결하는 방식과 달리, Local Region만을 대상으로 가중치를 학습하므로 파라미터 수가 훨씬 적으며, Parameter Sharing과 Sparse Connection의 이점을 갖습니다.

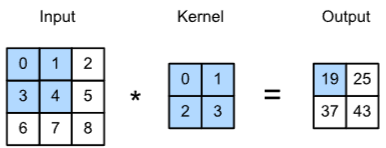
Cross-Correlation Operation

Cross-Correlation Operation1

주의: 딥러닝 라이브러리에서 구현된 “컨볼루션”은 정확히는 교차상관(cross-correlation) 연산이지만 관례상 컨볼루션이라고 부릅니다2.

1.2. Fully Connected Layer 방식과의 차이점

  • Fully Connected (FC)
    • 입력의 모든 뉴런과 출력 뉴런이 완전히 연결됩니다.
    • 예: 입력이 1000차원이라면, 출력 뉴런 100개 기준 가중치가 10만 개 필요.
    • Local Pattern과 무관하게 모든 위치를 동일 가중치로 연결합니다.

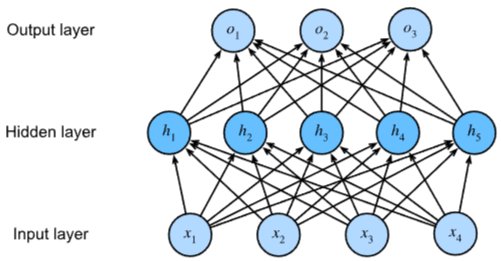
    Multilayer Perceptron

    Multilayer Perceptron3

  • Convolutional Layer
    • 입력의 Local Region(예: \(3 \times 3\))에 대해서만 학습 가중치를 적용합니다.
    • 커널을 이동하며, 동일한 가중치 세트를 모든 위치에 적용합니다.
    • 따라서 FC에 비해 파라미터 수가 훨씬 적고 효율적이며, 이미지의 공간적 구조를 살릴 수 있습니다4.

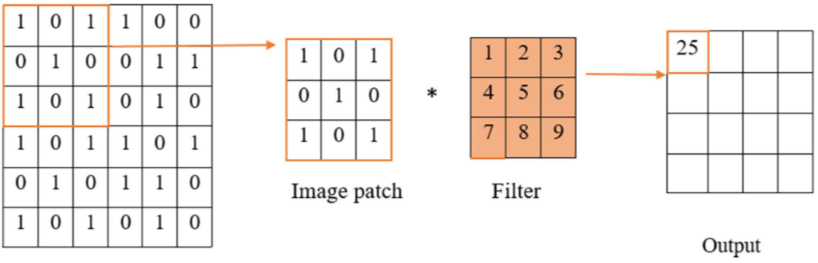
    Convolutional Layer

    Convolutional Layer3

2. 1차원 컨볼루션 레이어(1D Convolutional Layer)

2.1. 정의

1D 컨볼루션 레이어는 시간축을 따라 필터를 적용하는 방식입니다. 주로 시계열 데이터(신호 처리, 주가 예측, 센서 데이터 등)나 자연어 처리(NLP)에서 문장 시퀀스에 적용됩니다3.

2.2. 1차원 컨볼루션 레이어의 연산 방식

아래 수식은 1차원 컨볼루션 연산이 어떻게 이루어지는지를 나타냅니다.

\[[w \, ⊛ \, x](i) = \sum_{u=0}^{L-1} w_u x_{i+u}\]

여기서 각 기호가 의미하는 바를 하나씩 살펴보겠습니다.

  • 입력 신호 \(x\)와 커널 \(w\)
    • \(x\)는 입력 데이터(예: 시계열 데이터나 1차원 신호)를 나타냅니다.
    • \(w\)는 일정한 크기를 가진 커널 \(L\)로 학습 가능한 파라미터입니다.
  • 내적(dot product) 연산
    • 수식에서 \(\sum_{u=0}^{L-1}\)는 커널의 길이 \(L\)만큼 반복하며, 각 원소끼리의 곱을 모두 더한다는 의미입니다.
    • 즉, 위치 \(i\)에서 커널 \(w\)와 입력 \(x\)의 해당 구간 \(\{x_i, x_{i+1}, \ldots, x_{i+L-1}\}\) 간의 내적을 계산합니다.
  • 커널을 입력 위에서 슬라이딩
    • 연산은 입력 \(x\)의 각 가능한 위치 \(i\)에 대해 수행됩니다.
    • 예를 들어, \(i=0\)일 때는 \(x_0, x_1, \ldots, x_{L-1}\)와 \(w_0, w_1, \ldots, w_{L-1}\)의 내적,
      \(i=1\)일 때는 \(x_1, x_2, \ldots, x_{L}\)와의 내적을 구하는 방식입니다.
    • 이렇게 커널이 입력 데이터 위를 순차적으로 이동하면서 각각의 위치에서 동일한 방식으로 연산되어, 새로운 출력 신호가 생성됩니다.
  • 출력
    • 최종적으로, 각 위치 \(i\)에서 계산된 내적의 합이 출력 신호의 \(i\)번째 원소가 됩니다.
    • 이 출력은 입력 신호의 Local Feature를 추출하는 역할을 하며, 필터(커널)가 학습되는 과정에서 특정 패턴(예: 엣지, 주파수 특성 등)을 강조하도록 동작합니다.
  • 예시
    • 만약 커널 \(w\)의 길이가 3 (\(L=3\))이고, \(w = [w_0, w_1, w_2]\)이며, 입력 \(x\)가 \([x_0, x_1, x_2, x_3, \ldots]\)라고 한다면 아래와 같이 계산됩니다.
    • \(i=0\)일 때: \([w ⊛ x](0) = w_0 x_0 + w_1 x_1 + w_2 x_2\)
    • \(i=1\)일 때: \([w ⊛ x](1) = w_0 x_1 + w_1 x_2 + w_2 x_3\)

  • 1차원 컨볼루션 계산 예시(1채널) 1D Convolutional Layer 6.3.3 One-dimensional cross-correlation operation with single input channels3: \(0 \times 1 + 1 \times 2 = 2\)

  • 1차원 컨볼루션 계산 예시(3채널) 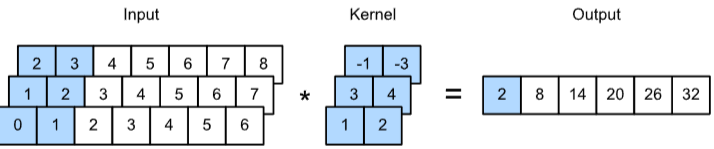1D Convolutional Layer with 3 Channels One-dimensional cross-correlation operation with 3 input channels3: \(0 \times 1 + 1 \times 2 + 1 \times 3 + 2 \times 4 + 2 \times (1) + 3 \times (3) = 2\)

2.3. 1차원 컨볼루션 레이어의 파라미터

  • in_channels: 입력 채널 수
  • kernel_size: 필터(커널)의 크기
  • filters: 출력 채널 수

2.4. 1차원 컨볼루션 레이어의 활용 예시

  • 자연어 처리 (NLP): 문장 시퀀스(임베딩)에서 n-gram 수준의 특징을 뽑아내 감정 분석, 분류 등에 활용.
  • 신호 처리 / 음성 처리: EEG, ECG, 오디오 파형 등 시간적 패턴을 가진 신호에서 특정 주파수 대역이나 Local Pattern을 학습.
  • 시계열 예측: 주가, 기상, 제조 공정 데이터 등 연속 데이터에서 국소적 변동을 포착.

3. 2차원 컨볼루션 레이어(2D Convolutional Layer)

3.1. 정의

2D 컨볼루션 레이어는 이미지와 같이 가로·세로의 2차원 그리드 형태 데이터를 처리합니다. 필터 역시 \(H \times W\) 형태를 갖고, 이미지의 각 Local Region(예: \(3 \times 3\))에 대해서 곱셈-덧셈 연산을 수행하여 Feature Map을 만듭니다.

  • 예: RGB 이미지(채널=3) → 필터 크기 \(H \times W\) × 채널 3 → 컨볼루션 후 하나의 출력 채널(feature map) 생성.
    여러 필터 사용 시 출력 채널 수가 증가합니다.

3.2. 2차원 컨볼루션 레이어의 연산 방식

아래 수식은 2차원 컨볼루션 연산이 입력 데이터(예: 이미지)에 대해 어떻게 이루어지는지를 보여줍니다.

\[[ W ⊛ X ]( i, j ) = \sum_{u=0}^{H-1} \sum_{v=0}^{W-1} w_{u,v} x_{i+u,j+v}\]

각 기호와 연산 과정을 하나씩 살펴보겠습니다.

  • 입력 \(X\)와 커널 \(W\)
    • 입력 \(X\): 2차원 행렬 형태의 데이터입니다. 예를 들어, 흑백 이미지라면 각 원소는 픽셀 값을 나타냅니다.
    • 커널 \(W\): \(H \times W\) 크기의 필터(또는 커널)입니다. 이 필터는 학습 가능한 파라미터로, 이미지의 특정 패턴(예: 엣지, 코너 등)을 감지하는 역할을 합니다.
  • 출력 \([W ⊛ X](i,j)\)
    • 출력 행렬의 각 위치 \((i, j)\)는 입력 \(X\)의 해당 영역과 커널 \(W\) 간의 내적(dot product) 결과입니다.
    • 즉, \(W\)를 \(X\)의 위치 \((i,j)\)에 맞춰 놓고, \(W\)의 각 원소 \(w_{u,v}\)와 \(X\)의 대응 원소 \(x_{i+u, j+v}\)를 곱한 후 모두 합산합니다.
  • 내적 연산의 상세 과정
    • 내부 합산:
      • \(\sum_{v=0}^{W-1} w_{u,v}\, x_{i+u,j+v}\)는 커널의 한 행에 대해 대응하는 입력 영역의 원소들과 곱셈 후 합산합니다.
      • \(\sum_{u=0}^{H-1} (\cdot)\)는 이러한 행별 결과를 모두 더해 최종 값을 계산합니다.
    • 슬라이딩 윈도우:
      • 커널 \(W\)는 입력 \(X\) 위에서 좌측 상단 모서리가 \((i, j)\)인 위치에 놓입니다.
      • 커널의 크기인 \(H \times W\)만큼의 영역을 입력에서 선택하여, 이 부분과 커널 간의 내적을 계산합니다.
      • 이 과정이 입력 전체에 대해 반복되어, 전체 출력 행렬(Feature Map)이 생성됩니다.
  • 의미와 역할
    • 지역적 특징(Local Feature) 추출:
      • 각 위치에서 커널과 입력 부분 영역의 내적은, 그 위치에서 지역적으로 중요한 특징(예: 엣지, 텍스처 등)을 반영합니다.
    • 공유 가중치(Weight Sharing):
      • 동일한 커널 \(W\)가 입력 전체에 대해 사용되므로, 동일한 패턴을 여러 위치에서 탐지할 수 있습니다.

  • 예시
    \(H = 3\), \(W = 3\) 크기의 커널과 이미지 \(X\)가 있다고 가정하면 출력 \((i,j)\)에서의 값은 \(3 \times 3\) 영역 내의 각 픽셀과 해당 커널 가중치의 곱의 합입니다.

    \[[W ⊛ X](i,j)\] \[= w_{0,0}\,x_{i,j} + w_{0,1}\,x_{i,j+1} + w_{0,2}\,x_{i,j+2} + \cdots + w_{2,2}\,x_{i+2,j+2}\]

  • 2차원 컨볼루션 계산 예시(1채널) 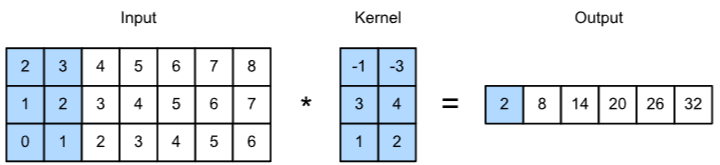2D Cross-Correlation Operation Two-dimensional cross-correlation operation with a single input channel.3

  • 2차원 컨볼루션 계산 예시(2채널) 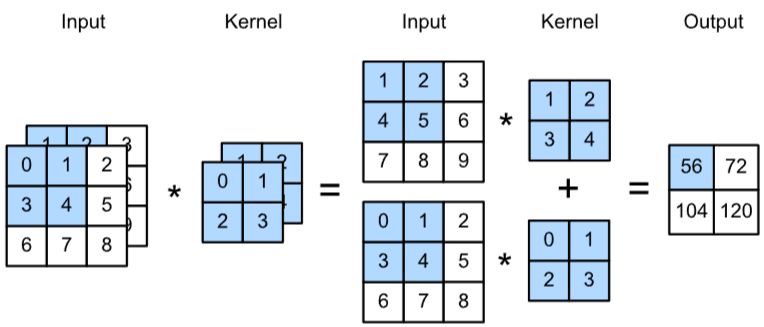2D Cross-Correlation Operation Two-dimensional cross-correlation operation with 2 input channels.3

3.3. 2차원 컨볼루션 레이어의 파라미터

  • 입력 채널(in_channels): RGB 이미지 → 3 등
  • 커널 크기(kernel_size): \(H \times W\)
  • 출력 채널(filters, out_channels): 필터 개수
  • 스트라이드(Stride), 패딩(Padding): 출력 크기를 조정, 가장자리 정보 손실 방지 등에 사용

3.4. 2차원 컨볼루션 레이어의 활용 예시

  • 이미지 분류, 객체 검출, 세그멘테이션 등 컴퓨터 비전 분야 전반
  • 의료 영상 분석, 자율주행 영상 처리, 산업용 결함 검출 등
  • 필터가 처음에는 에지나 코너 등을, 깊어질수록 보다 복합적인 형태(예: 눈, 얼굴, 특정 질감)를 학습합니다.

4. 행렬-벡터 곱셈(matrix-vector multiplication)을 이용한 컨볼루션 레이어의 연산

4.1. 행렬-벡터 곱셈을 이용한 연산 예시

  • 컨볼루션은 선형 연산자이기 때문에 행렬 곱셈으로 표현할 수 있습니다.
  • 아래 수식은 3 × 3 입력 X를 2 × 2 커널 W와 컨볼루션하여 2 × 2 출력 Y를 계산한 예시입니다.
\[Y = \begin{pmatrix} w_1 & w_2 \\ w_3 & w_4 \end{pmatrix} \odot \begin{pmatrix} x_1 & x_2 & x_3 \\ x_4 & x_5 & x_6 \\ x_7 & x_8 & x_9 \end{pmatrix}\] \[= \begin{pmatrix} (w_1 x_1 + w_2 x_2 + w_3 x_4 + w_4 x_5) \\ (w_1 x_2 + w_2 x_3 + w_3 x_5 + w_4 x_6) \\ (w_1 x_4 + w_2 x_5 + w_3 x_7 + w_4 x_8) \\ (w_1 x_5 + w_2 x_6 + w_3 x_8 + w_4 x_9) \end{pmatrix}\]
  • 이를 행렬곱셈으로 표현한 수식은 아래와 같습니다.
\[y = Cx\] \[= \begin{pmatrix} w_1 & w_2 & 0 & w_3 & w_4 & 0 & 0 & 0 & 0 \\ 0 & w_1 & w_2 & 0 & w_3 & w_4 & 0 & 0 & 0 \\ 0 & 0 & 0 & w_1 & w_2 & 0 & w_3 & w_4 & 0 \\ 0 & 0 & 0 & 0 & w_1 & w_2 & 0 & w_3 & w_4 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ x_8 \\ x_9 \end{pmatrix}\] \[= \begin{pmatrix} w_1 x_1 + w_2 x_2 + w_3 x_4 + w_4 x_5 \\ w_1 x_2 + w_2 x_3 + w_3 x_5 + w_4 x_6 \\ w_1 x_4 + w_2 x_5 + w_3 x_7 + w_4 x_8 \\ w_1 x_5 + w_2 x_6 + w_3 x_8 + w_4 x_9 \end{pmatrix}\]

위 수식은 2차원 컨볼루션 연산이 선형 연산자임을 이용하여, 이를 행렬-벡터 곱셈으로 표현하는 예시입니다. 아래에서 단계별로 자세히 설명하겠습니다.

4.2. 컨볼루션 연산 설명

  • 입력 \(X\)와 커널 \(W\)

    • 입력 \(X\):
      \(\begin{pmatrix} x_1 & x_2 & x_3 \\ x_4 & x_5 & x_6 \\ x_7 & x_8 & x_9 \end{pmatrix}\) 3 × 3 크기의 입력입니다.

    • 커널 \(W\):
      \(\begin{pmatrix} w_1 & w_2 \\ w_3 & w_4 \end{pmatrix}\) 2 × 2 크기의 필터(커널)로, 학습 가능한 가중치들이 포함되어 있습니다.

  • 컨볼루션 결과 \(Y\)
    커널을 입력 위에서 슬라이딩하면서 각 위치에서 내적(dot product)을 수행하게 됩니다. 커널이 3 × 3 입력 위에서 이동할 수 있는 위치는 총 4곳이 있고, 각각의 결과는 다음과 같이 계산됩니다.

    1. 첫 번째 위치:
      \(y_1 = w_1 x_1 + w_2 x_2 + w_3 x_4 + w_4 x_5\)

    2. 두 번째 위치:
      \(y_2 = w_1 x_2 + w_2 x_3 + w_3 x_5 + w_4 x_6\)

    3. 세 번째 위치:
      \(y_3 = w_1 x_4 + w_2 x_5 + w_3 x_7 + w_4 x_8\)

    4. 네 번째 위치:
      \(y_4 = w_1 x_5 + w_2 x_6 + w_3 x_8 + w_4 x_9\)

    이 네 결과를 모으면 최종 출력 \(Y\)는 2 × 2 형태의 값들을 갖게 됩니다.

4.3. 행렬-벡터 곱셈 설명

컨볼루션 연산은 선형 연산자이므로, 다음과 같이 행렬 곱셈 형태로 표현할 수 있습니다.

\[y = Cx\]
  • \(x\)는 입력 \(X\)를 벡터화한 것으로,
    \(x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \\ x_4 \\ x_5 \\ x_6 \\ x_7 \\ x_8 \\ x_9 \end{pmatrix}\)
  • \(C\)는 컨볼루션 연산을 수행하는 변환 행렬로, 각 행은 입력의 특정 패치(patch)와 커널 \(W\)의 가중치들을 대응시켜 내적을 수행하도록 구성되어 있습니다.

변환 행렬 \(C\)는 아래와 같이 구성됩니다.

\[C = \begin{pmatrix} w_1 & w_2 & 0 & w_3 & w_4 & 0 & 0 & 0 & 0 \\ 0 & w_1 & w_2 & 0 & w_3 & w_4 & 0 & 0 & 0 \\ 0 & 0 & 0 & w_1 & w_2 & 0 & w_3 & w_4 & 0 \\ 0 & 0 & 0 & 0 & w_1 & w_2 & 0 & w_3 & w_4 \end{pmatrix}\]
  • 첫 번째 행:
    • 해당 행은 입력의 첫 번째 패치 \(\{x_1, x_2, x_4, x_5\}\)에 대응합니다.
    • 따라서 \(w_1\)와 \(w_2\)는 \(x_1\)과 \(x_2\)에, \(w_3\)와 \(w_4\)는 \(x_4\)와 \(x_5\)에 곱해집니다.
  • 두 번째 행:
    • 입력의 두 번째 패치 \(\{x_2, x_3, x_5, x_6\}\)에 해당하여, \(w_1\)가 \(x_2\), \(w_2\)가 \(x_3\), \(w_3\)가 \(x_5\), \(w_4\)가 \(x_6\)에 대응합니다.
  • 세 번째 행:
    • 입력의 세 번째 패치 \(\{x_4, x_5, x_7, x_8\}\)에 해당합니다.
  • 네 번째 행:
    • 입력의 네 번째 패치 \(\{x_5, x_6, x_8, x_9\}\)에 해당합니다.

이와 같이 각 행은 해당 패치의 위치에 맞춰 커널의 가중치들을 배치하고, 나머지 자리는 0으로 채워집니다.

4.4. 행렬 곱셈을 통한 연산 과정

행렬 곱셈 \(y = Cx\)를 실제로 수행하면,

\[y = \begin{pmatrix} w_1 x_1 + w_2 x_2 + w_3 x_4 + w_4 x_5 \\ w_1 x_2 + w_2 x_3 + w_3 x_5 + w_4 x_6 \\ w_1 x_4 + w_2 x_5 + w_3 x_7 + w_4 x_8 \\ w_1 x_5 + w_2 x_6 + w_3 x_8 + w_4 x_9 \end{pmatrix}\]
  • 각 원소 \(y_i\)는 대응하는 입력 패치와 커널의 내적 결과입니다.
  • 예를 들어, 첫 번째 원소 \(y_1\)는 입력 벡터의 \(x_1, x_2, x_4, x_5\)와 커널 가중치 \(w_1, w_2, w_3, w_4\)의 곱의 합으로 구성됩니다.

이 결과는 앞서 컨볼루션으로 직접 계산한 출력과 동일하며, 이를 통해 컨볼루션 연산을 행렬 곱셈으로 표현할 수 있음을 알 수 있습니다.

4.5. 행렬-벡터 곱셈 방식의 장점

  • 최적화된 연산 라이브러리 활용:
    BLAS, CUDA의 cuBLAS 등 고도로 최적화된 행렬 곱셈 라이브러리를 사용할 수 있으므로, 일반적인 컨볼루션 연산보다 빠른 계산이 가능합니다.

  • 병렬 처리 및 하드웨어 가속:
    행렬 곱셈은 GPU 및 기타 하드웨어 가속기를 활용하여 병렬로 빠르게 처리할 수 있습니다.

  • 선형 연산의 단순화:
    컨볼루션을 행렬 곱셈으로 전개하면, 전체 연산 과정이 선형 연산으로 단순화되어 수학적 분석이나 최적화가 용이해집니다.

  • 메모리 사용 고려:
    입력 패치를 모두 추출하여 행렬 \(C\)를 구성하는 과정(im2col 기법 등)에서 메모리 사용량이 증가하는 단점이 있지만, 실제로는 최적화된 행렬 곱셈의 연산 속도가 이를 상쇄합니다.

참고문헌

  1. Hosny, K. M., Mortda, A. M., Fouda, M. M., & Lashin, N. A. (2022). An efficient CNN model to detect copy-move image forgery. IEEE Access, 10, 48622-48632. ↩

  2. Chollet, F. (2017). Xception: Deep Learning with Depthwise Separable Convolutions. CVPR Workshops, 1–9. ↩

  3. ZHANG, Aston, et al. (2021). Dive into deep learning. arXiv preprint arXiv:2106.11342. ↩ ↩2 ↩3 ↩4 ↩5 ↩6 ↩7

  4. Yu, F., & Koltun, V. (2015). Multi-Scale Context Aggregation by Dilated Convolutions. ICLR. ↩