[CNN] (4) 패딩(Padding)과 스트라이드(Stride)

5 minute read

이번 포스팅에서는 컨볼루션 레이어(Convolutional Layer)에서 패딩(Padding)과 스트라이드(Stride)에 대해서 다뤄보겠습니다.

CNN 시리즈

1. 패딩(Padding)의 이해

1.1. 패딩의 정의와 필요성

1.1.1. 패딩이란?

패딩이란 컨볼루션 연산 시 입력 데이터의 경계를 보존하기 위해 입력 배열의 가장자리에 여분의 픽셀을 추가하는 작업을 말합니다.
유효 영역만을 사용하는 경우 이미지의 픽셀이 줄어들기 때문에 이미지의 경계에 있는 중요한 정보를 잃을 수 있습니다.
예를들어 240 × 240 픽셀 이미지에 시작한다면, 5 × 5 컨볼루션이 10개의 레이어에 적용되면 이미지는 200 × 200 픽셀로 줄어들게 되며 이는 이미지의 30%를 잘라내고 원본 이미지의 경계에 있는 중요한 정보를 소멸시킬 수 있습니다.
Padding을 활용하면 컨볼루션 연산을 진행하면서 출력 크기를 유지하거나 경계 영역의 정보를 잃지 않도록 만들 수 있습니다. ¹ ².

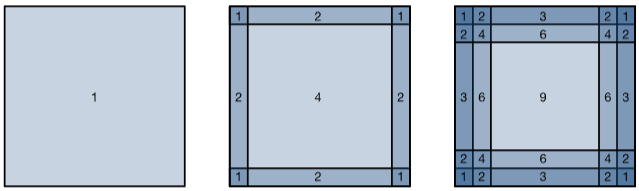
Example of Padding

Pixel utilization for convolutions of size 1 × 1, 2 × 2, and 3 × 3 respectively.¹

1.1.2. 패딩이 필요한 이유

경계 정보 손실 방지: 여러 층을 거치면서 이미지 혹은 Feature Map의 가장자리 픽셀이 소멸되는 현상 방지
출력 Feature Map의 크기 조절: 모델이 지나치게 축소되지 않도록 유지

1.1.3. CNN에서 패딩 적용

컨볼루션 신경망(CNN)은 일반적으로 1, 3, 5 또는 7과 같은 홀수 높이와 너비 값을 가진 컨볼루션 커널을 사용합니다.
홀수 커널 크기를 선택하는 것은 위와 아래에 같은 수의 행을 패딩하는 동시에 좌우에도 같은 수의 열을 패딩함으로써 차원을 보존할 수 있다는 장점이 있습니다.

1.2. Zero Padding

1.2.1. Zero Padding이란?

입력 경계에 0을 값으로 채워 넣는 방식
경계부 정보 포함 가능, 모델이 가장자리 특징까지 학습 가능

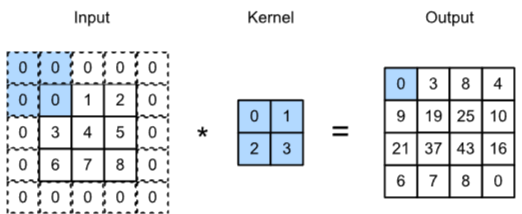
Zero Padding

Two-dimensional cross-correlation with padding¹

1.2.2. Same Convolution

출력 크기가 입력 크기와 동일한 컨볼루션 연산
Zero Padding을 사용하여 출력 크기를 유지

Same Convolution

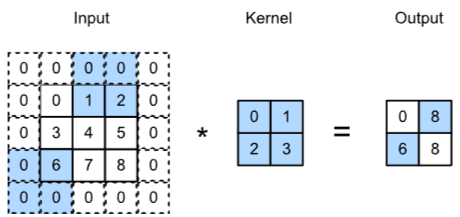
Same-convolution (using zero-padding) ensures the output is the same size as the input.³

1.2.2. Zero Padding의 수식

아래 수식은 일반적인 Zero Padding의 수식입니다.

\[(x_h + 2p_h - f_h + 1) \times (x_w + 2p_w - f_w + 1) \quad\]

입력: \(x_h \times x_w\)
커널: \(f_h \times f_w\)
패딩: \(p_h\)와 \(p_w\)

1.2.3. Zero Padding의 수식 예시

\(5 \times 7\) 크기의 입력 데이터에 대해 \(3 \times 3\) 커널을 사용하고 패딩을 1로 설정한 경우 출력 크기는 \(5 \times 7\)이 됩니다.

\[(5 + 2 - 3 + 1) \times (7 + 2 - 3 + 1) = 5 \times 7 \quad\]

입력 크기: \(x_h = 5\), \(x_w = 7\)
커널 크기: \(f_h = 3\), \(f_w = 3\)
패딩: \(p_h = 1\), \(p_w = 1\)

즉 스트라이드(아래에서 설명할 예정입니다.)가 1일 때 \(2p = f - 1\)로 설정하면 출력은 입력과 같은 크기를 갖게 됩니다.

1.3. 패딩이 Feature Map에 미치는 영향

1.3.1. 출력 크기 계산

가정: \(s(스트라이드)=1\)

\[n_{\text{out}} = n + 2P - k + 1 \quad\]

\(n\): 입력 크기
\(P\): 한쪽 당 패딩 수
\(k\): 커널(필터) 크기
예: 5×5 입력, 3×3 커널, \(P=1\)이면 → 출력 5×5

\[5 + 2*1 - 3 + 1 = 5\]

2. 스트라이드(Stride)의 이해

2.1. 스트라이드의 정의와 역할

2.1.1. 스트라이드란?

스트라이드(Stride)는 컨볼루션 연산에서 커널을 입력 텐서 위에 이동시킬 때 한 번에 이동하는 픽셀 수를 의미합니다.
출력 픽셀은 필터의 크기를 기준으로 입력의 가중 조합으로 생성됩니다. 입력이 겹치기 때문에 인접한 출력 값이 매우 유사해집니다. 이런 경우 매 \(s\)번째 입력을 건너뜀으로써 중복성을 줄이면서 생넝을 개선할 수 있습니다.
한 번에 1픽셀씩 이동시키는 것이 일반적이지만 때때로 성능을 개선하거나 다운샘플링을 원할 때 1픽셀 이상 이동할 수 있습니다.¹ ².

Stride

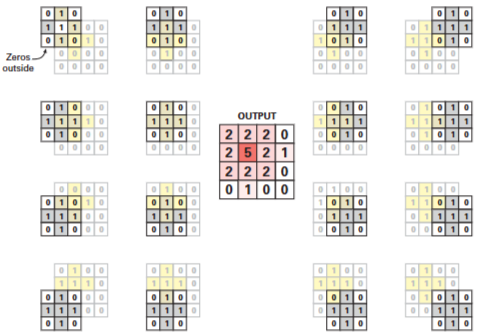
Cross-correlation with strides of 3 and 2 for height and width, respectively.¹

2.1.2. 스트라이드의 역할

계산 효율 개선: 계산량 감소에 따른 연산 효율을 얻을 수 있음
다운샘플링 효과: 스트라이드가 커지면 출력 Feature Map 크기가 작아져서 다운 샘플링 효과를 얻을 수 있음

2.1.3. 스트라이드의 구성

Vertical Stride: 세로 방향으로 커널이 이동하는 픽셀 수
Horizontal Stride: 가로 방향으로 커널이 이동하는 픽셀 수

2.2. 스트라이드가 Feature Map 크기에 미치는 영향

2.2.1. 스트라이드의 출력 계산 공식²

\[\left[ \frac{x_h + 2p_h - f_h + s_h}{s_h} \right] \times \left[ \frac{x_w + 2p_w - f_w + s_w}{s_w} \right]\]

\({s_h}\): 높이에 대한 스트라이드
\({s_w}\): 너비에 대한 스트라이드
\(x_h\): 입력 높이
\(x_w\): 입력 너비
\(p_h\): 위아래 패딩
\(p_w\): 좌우 패딩
\(f_h\): 필터(커널) 높이
\(f_w\): 필터(커널) 너비

2.2.2. 스트라이드의 출력 계산 예시

아래 예시 이미지의 (b)를 계산한 결과는 아래와 같습니다.

입력 높이: \(x_h = 5\)
입력 너비: \(x_w = 7\)
필터(커널) 높이: \(f_h = 3\)
필터(커널) 너비: \(f_w = 3\)
위아래 패딩: \(p_h = 1\)
좌우 패딩: \(p_w = 1\)
높이에 대한 스트라이드: \(s_h = 2\)
너비에 대한 스트라이드: \(s_w = 2\)

\[\left\lfloor \frac{5 + 2 - 3 + 2}{2} \right\rfloor \times \left\lfloor \frac{7 + 2 - 3 + 2}{2} \right\rfloor\] \[= \left\lfloor \frac{6}{2} \right\rfloor \times \left\lfloor \frac{4}{1} \right\rfloor\] \[= 3 \times 4\]

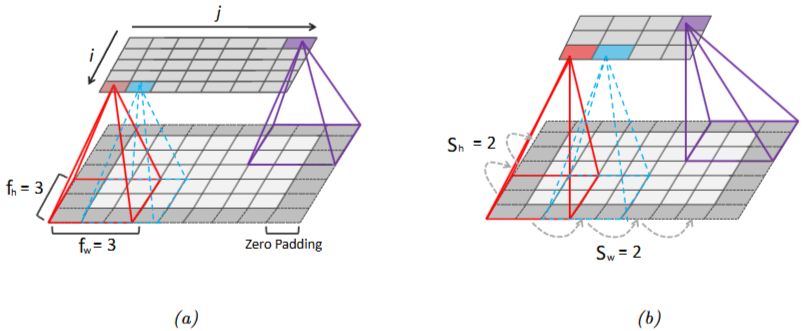
Zero Padding Example

lustration of padding and strides in 2d convolution. (a) We apply “same convolution” to a 5 × 7 input (with zero padding) using a 3 × 3 filter to create a 5 × 7 output. (b) Now we use a stride of 2, so the output has size 3 × 4.⁴

3. 예시 코드

아래 파이썬 코드는 Padding과 Stride를 적용해서 2D 컨볼루션 연산을 진행한 예시입니다.

import torch
import torch.nn.functional as F
import pandas as pd


def convolve2D(image, kernel, padding=0, stride=1):
    """
    PyTorch의 conv2d 함수를 사용하여 2D Convolution 연산을 수행합니다.

    Parameters:
        image (torch.Tensor): 2차원 입력 이미지 텐서.
        kernel (torch.Tensor): 2차원 컨볼루션 필터 텐서.
        padding (int): 이미지의 테두리에 추가할 0 패딩 두께.
        stride (int): 필터가 이동하는 보폭.

    Returns:
        torch.Tensor: 컨볼루션 결과 (2D 텐서).
    """
    # 입력 이미지의 shape을 (batch, channel, H, W)로 변경
    image_tensor = image.unsqueeze(0).unsqueeze(0)  # shape: (1, 1, H, W)
    # 커널의 shape을 (out_channels, in_channels, kH, kW)로 변경
    kernel_tensor = kernel.unsqueeze(0).unsqueeze(0)  # shape: (1, 1, kH, kW)

    # conv2d 연산 수행
    output = F.conv2d(
        image_tensor, kernel_tensor, bias=None, stride=stride, padding=padding
    )
    return output.squeeze()


if __name__ == "__main__":
    # 4x4 입력 이미지 (예시)
    input_image = torch.tensor(
        [[1, 1, 1, 1], [1, 0, 0, 1], [1, 0, 0, 1], [1, 1, 1, 1]],
        dtype=torch.float32,
    )

    # 3x3 커널 (예시: horizontal edge 검출용)
    kernel = torch.tensor([[1, 0, 1], [1, 0, 1], [1, 0, 1]], dtype=torch.float32)

    # "Same convolution": padding=1, stride=1 로 설정하면 출력 크기가 입력과 동일(4x4)해집니다.
    output1 = convolve2D(input_image, kernel, padding=0, stride=1)
    output2 = convolve2D(input_image, kernel, padding=1, stride=1)
    output3 = convolve2D(input_image, kernel, padding=1, stride=2)

    print("입력 이미지:")
    print(pd.DataFrame(input_image.int().tolist()).to_string(index=False, header=False))

    print("\n커널:")
    print(pd.DataFrame(kernel.int().tolist()).to_string(index=False, header=False))

    print("\n출력 (패딩=0, 스트라이드=1)")
    print(pd.DataFrame(output1.int().tolist()).to_string(index=False, header=False))
    print("\n출력 (패딩=1, 스트라이드=1)")
    print(pd.DataFrame(output2.int().tolist()).to_string(index=False, header=False))
    print("\n출력 (패딩=1, 스트라이드=2)")
    print(pd.DataFrame(output3.int().tolist()).to_string(index=False, header=False))

# 실행 결과

입력 이미지:
1 1 1
0 0 1
0 0 1
1 1 1

커널:
0 1
0 1
0 1

출력 (패딩=0, 스트라이드=1)
4
4

출력 (패딩=1, 스트라이드=1)
3 3 1
4 4 1
4 4 1
3 3 1

출력 (패딩=1, 스트라이드=2)
3
4

패딩=0, 스트라이드=1: Feature Map 크기가 2×2 로 작아짐
패딩=1, 스트라이드=1: Feature Map 크기가 원본 입력(4×4)와 동일하게 유지됨
패딩=1, 스트라이드=2: Feature Map 크기가 2×2 로 작아짐(다운샘플링 효과)

위 코드 결과를 보면, 패딩이 없으면 경계 정보를 일부 잃고 출력 크기가 작아지는 반면, 패딩을 주면 출력 Feature Map이 커지고 가장자리 부분에도 출력이 생기는 것을 확인할 수 있습니다. 스트라이드를 늘리면 연산 간격이 커져 출력 크기가 작아지며, 이는 다운샘플링(downsampling) 효과를 일으킵니다.

참고문헌

Zhang, A., Lipton, Z. C., Li, M., & Smola, A. J. (2021). Dive into deep learning. arXiv preprint arXiv:2106.11342. ↩ ↩² ↩³ ↩⁴ ↩⁵
Murphy, K. P. (2012). Machine learning: a probabilistic perspective. MIT press. ↩ ↩² ↩³
Stevens, E., Antiga, L., & Viehmann, T. (2020). Deep learning with PyTorch. Manning Publications. ↩
Géron, A. (2022). Hands-on machine learning with Scikit-Learn, Keras, and TensorFlow. O’Reilly Media, Inc. ↩

Share on

Twitter Facebook