[CNN] (6) 정규화 레이어(Normalization Layer)

9 minute read

이번 포스팅에서는 정규화 레이어(Normalization Layer)에 대해 알아보겠습니다.

CNN 시리즈Permalink

1. 정규화 레이어(Normalization Layer)의 기본 개념Permalink

1.1 정규화 레이어란?Permalink

딥러닝 모델에서 정규화(Normalization)는 신경망의 각 층 입력 분포를 재조정하여 학습을 안정화하고 기울기(Gradient) 흐름을 원활하게 하는 핵심 기법입니다.
정규화 레이어는 활성화 함수를 전후로 각 채널·공간·샘플 축에 대한 통계를 활용해 분포를 일정 범위로 맞춤으로써, 가중치가 지나치게 커지거나 작아지는 문제를 완화할 수 있습니다.

1.2 정규화 레이어의 필요성Permalink

딥러닝 모델을 훈련할 때 그래디언트가 매우 작아지는 소실(Vanishing) 문제와 반대로 매우 커지는 폭주(Exploding) 문제로 인해 네트워크가 깊어질수록 학습이 어려워질 수 있습니다.
정규화 레이어는 입력의 통계를 적절히 맞춤으로써 기울기가 지나치게 커지거나 작아지는 현상을 완화하고, 학습을 안정시키는 효과가 있습니다.

1.3 정규화(Normalization)의 역할Permalink

그래디언트 소실/폭주 문제 해결 및 완화
기울기 흐름 안정화로 모델 학습 수렴이 빨라짐
가중치 초기값에 대한 민감도 감소
미니배치별 통계 차이가 규제(regularization) 효과를 유발

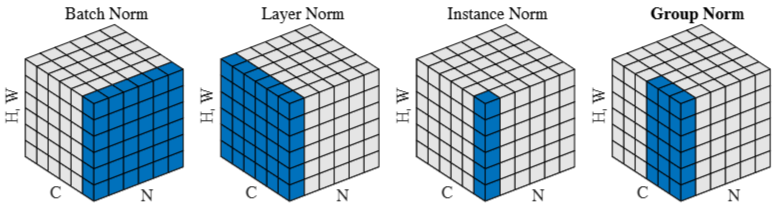
Normalization

Illustration of different activation normalization methods for a CNN. Each subplot shows a feature map tensor, with N as the batch axis, C as the channel axis, and (H, W) as the spatial axes. The pixels in blue are normalized by the same mean and variance, computed by aggregating the values of these pixels. Left to right: batch norm, layer norm, instance norm, and group norm (with 2 groups of 3 channels). ¹

2. Batch Normalization (BN)Permalink

2.1. Batch Normalization의 기본 개념Permalink

미니배치 단위로 정규화
BN은 학습 시 사용하는 미니배치(minibatch) 내에서 각 활성화의 평균(μ_B)와 분산(σ_B²)을 계산합니다.
정규화 후 재조정 (Scale & Shift)
계산된 평균과 분산을 사용해 Activation Function 출력을 표준화한 뒤, 학습 가능한 두 파라미터 γ (감마)와 β (베타)를 통해 다시 조정합니다.
- γ: 스케일(크기 조정)
- β: 시프트(위치 조정)
컨볼루션 층에서의 적용
만약 입력 텐서의 차원이 (N, C, H, W)라면,
- N: 배치 크기
- C: 채널 수
- H, W: 공간적 차원
  BN은 각 채널(c)을 고정하고, 배치 축(N) + 공간 축(H, W)을 합쳐 평균과 분산을 계산합니다.

추론 시 주의
학습 단계에서의 미니배치 통계를 그대로 쓰면, 추론 시 배치 크기가 1이거나 다른 환경일 때 문제가 생길 수 있습니다.
따라서 일반적으로 running mean과 running variance(지수 이동 평균으로 추정)를 업데이트해두었다가, 추론(inference) 단계에서는 이 값을 사용합니다.

2.2. Batch Normalization의 수식Permalink

2.2.1 최종 출력: 이동 및 축척된 활성화Permalink

\[\tilde{z}_n = \gamma \odot \hat{z}_n + \beta\]

\(\tilde{z}_n\): 최종 출력 활성화 벡터 (BN 레이어의 출력)
\(\hat{z}_n\): 표준화된(정규화된) 활성화 벡터
\(\gamma\): 학습 가능한 스케일 파라미터
\(\beta\): 학습 가능한 시프트 파라미터
\(\odot\): 원소별(element-wise) 곱셈

2.2.2. 표준화 과정: 평균과 분산으로 정규화Permalink

\[\hat{z}_n = \frac{z_n - \mu_B}{\sqrt{\sigma_B^2 + \epsilon}}\]

\(z_n\): 현재 레이어의 원래 활성화 벡터
\(\mu_B\): 미니배치 내의 활성화 평균
\(\sigma_B^2\): 미니배치 내의 활성화 분산
\(\epsilon\): 아주 작은 상수 (분모가 0이 되는 것을 방지)

2.2.3. 미니배치 평균 & 분산의 계산Permalink

\[\mu_B = \frac{1}{|B|} \sum_{z \in B} z\] \[\sigma_B^2 = \frac{1}{|B|} \sum_{z \in B} (z - \mu_B)^2\]

\(B\): 해당 미니배치
\(\mid B \mid\): 미니배치에 포함된 데이터(또는 활성화)의 개수

2.2.4. 역전파 시 미분 가능성Permalink

이 모든 과정은 미분 가능하게 설계되어 있어, 역전파(backpropagation)를 통해 BN 레이어의 입력 \(\mathbf{z}_n\)과 학습 파라미터 \(\gamma, \beta\)에 기울기가 전달될 수 있습니다.

2.3 Batch Normalization의 특징Permalink

장점
- 학습 안정화 및 가속: 내부 활성화 분포가 상대적으로 일정해짐
- 어느 정도 규제(regularization) 효과
- 대규모 배치에서 표준 기법으로 널리 사용
단점
- 배치 크기가 너무 작으면 통계가 제대로 추정되지 않아 성능 저하
- 분산 학습 시 모든 워커(worker)의 배치 통계를 동기화해야 하는 번거로움
- 추론(inference) 단계에서는 running mean/variance를 사용해야 함

3. Layer Normalization (LN)Permalink

3.1 Layer Normalization이란?Permalink

Layer Normalization은 한 샘플(배치 중 1개)에 대한 모든 활성화(채널+공간 축) 통계를 이용합니다.²

RNN이나 Transformer 등에서는 배치 크기가 제각각이거나 시퀀스 길이가 다르므로 BN 사용이 비효율적일 수 있습니다.
LN은 “한 샘플 내부”만을 기준으로 정규화하므로, 배치 크기에 의존하지 않는 장점이 있습니다.

3.2 Layer Normalization의 수식Permalink

배치 차원 \(N\), 채널 차원 \(C\), 공간 차원 \(H, W\)가 있을 때 샘플 \(n\)에 대한 평균 \(\mu_n\)과 분산 \(\sigma_n^2\)는 다음과 같이 구합니다.

\[\mu_n = \frac{1}{C \cdot H \cdot W} \sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^{W} x_{n,c,h,w}\] \[\sigma_n^2 = \frac{1}{C \cdot H \cdot W} \sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^{W} \bigl(x_{n,c,h,w} - \mu_n\bigr)^2\]

이후 \(\hat{x}_{n,c,h,w}\)를 아래와 같이 정규화하고, 채널별(또는 요소별) 학습 파라미터 \(\gamma_c, \beta_c\)로 다시 조정합니다.

\[\hat{x}_{n,c,h,w} = \frac{x_{n,c,h,w} - \mu_n}{\sqrt{\sigma_n^2 + \epsilon}}\] \[y_{n,c,h,w} = \gamma_{c} \,\hat{x}_{n,c,h,w} + \beta_{c}\]

3.3 Layer Normalization의 특징Permalink

배치 크기에 독립적
RNN/Transformer 등에서 표준처럼 사용
CNN에서 공간 차원 \((H, W)\)이 매우 큰 경우엔 BN보다 성능이 떨어질 수 있다는 보고도 있음

4. Instance Normalization (IN)Permalink

4.1 Instance Normalization이란?Permalink

Instance Normalization은 한 장의 이미지(샘플)에서 채널별로 평균과 분산을 계산하는 방식입니다.³⁴

Style Transfer나 GAN의 생성자(Generator)에서 이미지 스타일 정보를 제거·통일하기 위해 자주 활용됩니다.

4.2 Instance Normalization의 수식Permalink

\[\mu_{n,c} = \frac{1}{H \cdot W} \sum_{h=1}^{H}\sum_{w=1}^{W} x_{n,c,h,w}\] \[\sigma_{n,c}^2 = \frac{1}{H \cdot W} \sum_{h=1}^{H}\sum_{w=1}^{W} \bigl(x_{n,c,h,w} - \mu_{n,c}\bigr)^2\] \[\hat{x}_{n,c,h,w} = \frac{x_{n,c,h,w} - \mu_{n,c}}{\sqrt{\sigma_{n,c}^2 + \epsilon}}\] \[y_{n,c,h,w} = \gamma_c \,\hat{x}_{n,c,h,w} + \beta_c\]

4.3 Instance Normalization의 특징Permalink

장점
- 이미지 한 장 내의 스타일 특성을 제거하기 쉬움
- 배치 크기와 무관
단점
- 채널 간 상호작용은 전혀 고려하지 못함
- 분류/검출 등 일반적 CNN 작업에서는 BN/LN 대비 성능이 낮을 수 있음

5. Group Normalization (GN)Permalink

5.1 Group Normalization이란?Permalink

Group Normalization은 채널을 여러 그룹으로 나누어, 각 그룹 내에서 평균과 분산을 계산하는 방식입니다.²

LN(채널 전체)과 IN(채널 1개)의 절충안
작은 배치 크기에서도 BN 못지않은 성능을 보여 관심을 받음

5.2 Group Normalization의 수식Permalink

채널 수 \(C\)를 \(G\)개 그룹으로 나누었다고 할 때, 그룹 \(g\)에 속한 채널 집합을 \(C_g\)라 하면:

\[\mu_{n,g} = \frac{1}{|C_g| \cdot H \cdot W} \sum_{c \in C_g}\sum_{h=1}^{H}\sum_{w=1}^{W} x_{n,c,h,w}\] \[\sigma_{n,g}^2 = \frac{1}{|C_g| \cdot H \cdot W} \sum_{c \in C_g}\sum_{h=1}^{H}\sum_{w=1}^{W} \bigl(x_{n,c,h,w} - \mu_{n,g}\bigr)^2\]

정규화 후, 채널별로 다른 \(\gamma_c, \beta_c\)를 적용해 최종 출력 \(y_{n,c,h,w}\)를 얻습니다.

5.3 특징Permalink

장점
- 배치 크기에 의존하지 않음
- LN(그룹=전체 채널)과 IN(그룹=1) 사이를 유연하게 조절
- 소규모 배치, Detection/Segmentation 등에 강점
단점
- BN 대비 연산량·메모리 오버헤드가 다소 증가
- 적절한 그룹 수 \(G\)를 선택해야 함

6. 기타 정규화 기법들Permalink

Weight Normalization: 가중치 \(\mathbf{w}\)를 크기 \(g\)와 방향 \(\mathbf{v}\)로 분리(\(\mathbf{w} = g \frac{\mathbf{v}}{\|\mathbf{v}\|}\))하여 배치 통계 없이 학습 안정화를 꾀하는 방식.⁵
Batch-Instance Normalization (BIN): BN과 IN을 가중합으로 결합한 형태.
Switchable Normalization (SN): BN, LN, IN 통계를 모두 계산 후, 학습 가능한 게이트로 혼합 사용.⁶
Spectral Normalization: GAN 훈련 시 판별자의 기울기 폭주를 막기 위해 가중치 행렬의 최대 고유값을 1로 정규화.⁵

Local Response Normalization(LRN), Weight Standardization 등도 제안된 바 있지만, BN, LN, IN, GN이 현재 가장 널리 사용됩니다.

7. 정규화 레이어의 장점과 단점Permalink

정규화 기법	통계 계산 범위	배치 의존성	계산/메모리 비용	장점 및 용도
Batch Norm (BN)	동일 채널의 배치 전체 + 공간 전체	있음	낮음 (프레임워크 최적화) 분산 학습 시 통신 필요	– 학습 가속, 규제 효과 – ImageNet 등 대규모 배치 모델에서 표준
Layer Norm (LN)	한 샘플의 모든 채널+공간	없음	낮음	– 배치 크기 무관 – RNN, Transformer 등에 필수 – 온라인 러닝/강화학습에도 적합
Instance Norm (IN)	한 샘플의 채널별(공간만 통합)	없음	낮음	– 이미지별 스타일 제거 – Style Transfer, GAN 생성자
Group Norm (GN)	한 샘플의 채널 그룹(공간 통합)	없음	BN 대비 다소 높음	– 소규모 배치에서 BN 대체 – Detection/Segmentation 등 – LN↔IN 사이 유연 조절 가능
Switchable Norm (SN)	BN, LN, IN 혼합	경우에 따라 다름	계산량↑ (3종 통계 동시 계산)	– Adaptive 정규화 – 배치 크기/작업 도메인 변화에도 일관된 성능 – 일부 연구 모델에 시험적 적용

8. CNN에서의 정규화 레이어 구현과 역할Permalink

8.1 실제 CNN 구조에서의 활용Permalink

BatchNorm
- ResNet, Inception, VGG-BN 등 대부분의 이미지 분류 모델에서 필수 요소
- 일반적으로 (Conv → BN → 활성화(ReLU)) 순으로 블록을 구성
- 대규모 배치에서 뛰어난 성능과 규제 효과로 과적합 방지
- 추론 단계에서는 running mean/variance를 사용
BN 대안
- 배치 크기가 매우 작거나 실시간 예측 등으로 BN 통계가 불안정할 때 → Layer Norm 또는 Group Norm
- RNN/Transformer 구조 → Layer Norm이 사실상 표준
- Style Transfer, GAN 생성자 → Instance Norm

8.2 PyTorch 예시 코드Permalink

아래 코드는 “전역(mean, var) 정규화 + 스케일·시프트” 과정을 간단히 시연한 예시입니다.
실제 BN/LN/IN/GN은 (N, C, H, W)에서 통계를 구하는 범위가 달라질 뿐, 기본적으로 평균·분산으로 표준화 후 Scale & Shift한다는 핵심 아이디어는 동일합니다.

import torch
import pandas as pd

if __name__ == "__main__":
    # 4x4 입력 이미지 (예시)
    input_image = torch.tensor(
        [
            [0, 0, 1, 5],
            [0, 1, 5, 1],
            [1, 5, 1, 0],
            [5, 1, 0, 0],
        ],
        dtype=torch.float32,
    )

    # ----------------------------------
    # 1. 입력 이미지 출력
    # ----------------------------------
    print("=== 1. 입력 이미지 (4x4 픽셀) ===")
    print(pd.DataFrame(input_image.int().tolist()).to_string(index=False, header=False))

    # ----------------------------------
    # 2. 평균 (μ) 계산
    # ----------------------------------
    mu = input_image.mean()
    print("\n=== 2. 평균 (μ) 계산 ===")
    print("모든 픽셀의 평균 =", round(mu.item(), 3))

    # ----------------------------------
    # 3. 분산 (σ²) 계산
    # ----------------------------------
    sigma2 = input_image.var(unbiased=False)
    print("\n=== 3. 분산 (σ²) 계산 ===")
    print("모든 픽셀의 분산 =", round(sigma2.item(), 3))

    # ----------------------------------
    # 4. 표준화 (ẑ) 수행
    # ----------------------------------
    epsilon = 1e-5
    standardized = (input_image - mu) / torch.sqrt(sigma2 + epsilon)
    print("\n=== 4. 표준화 (ẑ) 수행 ===")
    print("계산식: (입력값 - 평균) / sqrt(분산 + ε)")
    print(pd.DataFrame(standardized.tolist()).to_string(index=False, header=False))

    # ----------------------------------
    # 5. Scale & Shift 적용
    # ----------------------------------
    gamma = 2.0
    beta = 0.5
    normalized = gamma * standardized + beta
    print("\n=== 5. Scale & Shift 적용 ===")
    print("γ = {}, β = {}".format(gamma, beta))
    print(pd.DataFrame(normalized.tolist()).to_string(index=False, header=False))

# 출력 예시
=== 1. 입력 이미지 (4x4 픽셀) ===
0 0 1 5
0 1 5 1
1 5 1 0
5 1 0 0

=== 2. 평균 (μ) 계산 ===
모든 픽셀의 평균 = 1.625

=== 3. 분산 (σ²) 계산 ===
모든 픽셀의 분산 = 3.984

=== 4. 표준화 (ẑ) 수행 ===
-0.814091 -0.814091 -0.313112  1.690803
-0.814091 -0.313112  1.690803 -0.313112
-0.313112  1.690803 -0.313112 -0.814091
 1.690803 -0.313112 -0.814091 -0.814091

=== 5. Scale & Shift 적용 ===
γ = 2.0, β = 0.5
-1.128181 -1.128181 -0.126224  3.881607
-1.128181 -0.126224  3.881607 -0.126224
-0.126224  3.881607 -0.126224 -1.128181
 3.881607 -0.126224 -1.128181 -1.128181

9. 최근 연구 동향: 적응형 정규화와 Transformer 정규화Permalink

적응형 정규화(Adaptive Normalization)
- Switchable Normalization (SN), Batch-Instance Normalization (BIN) 등
- Style Transfer 분야에서의 Adaptive Instance Normalization (AdaIN) 등
  - 콘텐츠 이미지의 특성맵을 스타일 이미지 통계로 정규화하여, 스타일 전이를 자연스럽게 구현³⁴.
Transformer 중심 정규화 기법
- Transformer에서는 일반적으로 Layer Norm을 사용
- RMS Norm: 평균을 빼는 대신 RMS(제곱평균제곱근)만으로 정규화해 계산 효율성을 높임
- Pre-LN vs Post-LN: 정규화를 Attention/FFN 이전(pre) 또는 이후(post)에 적용해 모델 안정성과 성능 차이를 유발
Normalization-Free Networks
- 정규화 레이어 없이도 학습을 안정화하려는 시도 (특정 활성화 함수, 가중치 초기화 기법, gradient clipping 등)
- 그러나 현재까지는 여전히 정규화 레이어를 쓰는 모델이 학습 속도와 최종 성능 면에서 유리하다는 결과가 많음

10. 정리Permalink

정규화 레이어(Normalization Layer)는 딥러닝 모델에서 안정적 학습과 성능 향상을 위해 사실상 필수적인 존재가 되었습니다.

Batch Normalization
- 대규모 데이터·배치 환경에서 학습 가속 및 규제 효과가 커서 CNN의 표준이 됨
- 추론 시에는 별도의 running mean/variance 사용
Layer Normalization, Group Normalization, Instance Normalization
- 배치 크기가 작거나 RNN/Transformer와 같이 배치 간 상호작용이 어렵거나 불필요할 때 대안
- Style Transfer, GAN 등의 특수 작업에서는 IN이 활용도 높음
적응형 정규화(Adaptive Normalization), Normalization-Free 같은 연구가 계속되고 있지만, 현재는 프로젝트 특성에 맞춰 BN, LN, IN, GN 중 하나(혹은 여러 기법 혼합)를 사용하는 것이 일반적

결국 모델의 데이터 규모, 작업 특성, 하드웨어 환경 등을 고려하여 가장 효율적인 정규화 전략을 세우는 것이 핵심입니다.

참고문헌Permalink

Wu, Y., & He, K. (2018). Group Normalization. Proceedings of the European Conference on Computer Vision (ECCV). ↩
Wu, Y., & He, K. (2018). Group Normalization. European Conference on Computer Vision (ECCV). ↩ ↩²
Huang, X., & Belongie, S. (2017). Arbitrary Style Transfer in Real-time with Adaptive Instance Normalization. ICCV. ↩ ↩²
Ulyanov, D., Vedaldi, A., & Lempitsky, V. (2016). Instance Normalization: The Missing Ingredient for Fast Stylization. arXiv preprint arXiv:1607.08022. ↩ ↩²
Ioffe, S., & Szegedy, C. (2015). Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. Proceedings of the 32nd International Conference on Machine Learning (ICML). ↩ ↩²
Luo, P., et al. (2018). Differentiable Learning-to-Normalize via Switchable Normalization. International Conference on Learning Representations (ICLR). ↩

Share on

Twitter Facebook