4 minute read

퍼셉트론은 인공 신경망의 가장 기본적인 구성 요소로, 단순한 선형 분류 문제를 해결하는 모델입니다. 1958년 프랭크 로젠블라트(Frank Rosenblatt)에 의해 제안되었으며, 생물학적인 뉴런의 작동 방식을 본떠 만들어졌습니다. 퍼셉트론은 여러 개의 입력 값을 받아 이들의 가중합을 계산하고, 활성화 함수(주로 계단 함수)를 통해 이진 분류를 수행합니다.

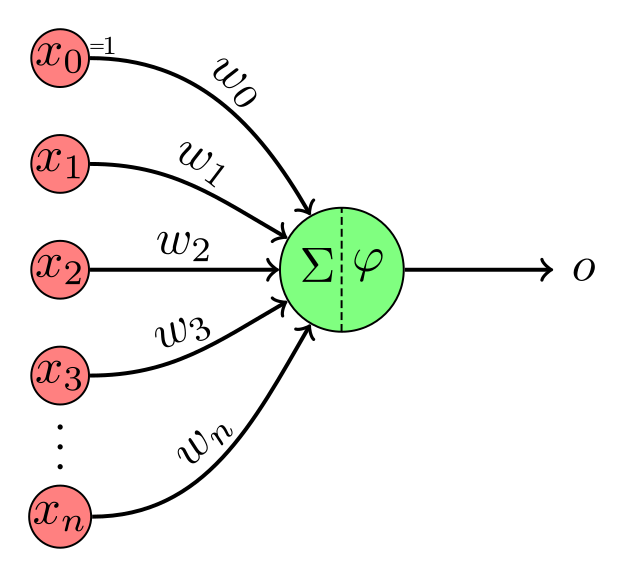
Perceptron Units

퍼셉트론의 기본 구조

퍼셉트론은 입력층과 출력층으로만 구성된 매우 단순한 신경망 구조를 가지고 있으며, 이는 한 개의 뉴런으로 이루어진 모델입니다. 퍼셉트론의 기본적인 구조는 다음과 같습니다:

  1. 입력층(Input Layer): 퍼셉트론의 입력 값은 $x_1, x_2, …, x_n$으로 표현됩니다. 각 입력 값은 해당 입력에 대한 가중치 $w_1, w_2, …, w_n$와 함께 사용됩니다.

  2. 가중치(Weights): 퍼셉트론은 각 입력에 대해 가중치 $w_i$를 적용하여 입력 값의 중요도를 결정합니다. 가중치는 학습 과정에서 조정되며, 가중치에 따라 모델의 예측이 달라집니다.

  3. 편향(Bias): 퍼셉트론에는 편향(bias) $b$가 포함되어 있습니다. 편향은 모델이 입력 값이 0일 때도 어느 정도 활성화되도록 하여 임계값을 조정하는 역할을 합니다.

  4. 가중합(Summation): 퍼셉트론은 입력 값에 가중치를 곱한 후 이를 모두 더한 값을 계산합니다. 이 값은 다음과 같이 표현됩니다:

    \[z = w_1x_1 + w_2x_2 + \cdots + w_nx_n + b\]

    즉, 각 입력의 가중합을 구하는 것입니다.

  5. 활성화 함수(Activation Function): 퍼셉트론의 출력 값은 활성화 함수를 통해 결정됩니다. 기본 퍼셉트론에서는 계단 함수(Step Function)를 활성화 함수로 사용하여 입력 값의 가중합이 임계값을 넘으면 1, 그렇지 않으면 0을 출력합니다. 이는 이진 분류 문제에 적합한 방식입니다.

    계단 함수는 다음과 같이 정의됩니다:

\[f(z) = \begin{cases} 1, & \text{if } z \geq 0 \\ 0, & \text{if } z < 0 \end{cases}\]

이 함수는 퍼셉트론이 선형 결정 경계를 기준으로 데이터를 두 개의 클래스로 나누는 것을 의미합니다.

퍼셉트론의 동작 원리

  1. 입력 값 전달 및 가중합 계산: 주어진 입력 값들과 각 입력에 대한 가중치가 결합하여 가중합을 계산합니다.
  2. 활성화 함수 적용: 가중합이 임계값을 넘는지 여부에 따라 활성화 함수가 적용됩니다. 기본 퍼셉트론의 경우 계단 함수를 사용하여 임계값을 넘으면 출력 1, 그렇지 않으면 출력 0을 반환합니다.
  3. 출력: 퍼셉트론은 이진 분류 문제에서 두 가지 클래스로 데이터를 분류하는 방식으로 동작합니다. 따라서 출력은 0 또는 1이 됩니다.

퍼셉트론의 학습

퍼셉트론은 지도 학습(Supervised Learning) 방식으로 학습하며, 주어진 입력과 출력 데이터를 이용하여 가중치와 편향을 조정합니다. 학습 과정은 다음과 같습니다:

  1. 초기화: 가중치 $w_1, w_2, \cdots, w_n$와 편향 $b$를 무작위 값이나 작은 값으로 초기화합니다.
  2. 순전파(Forward Propagation): 입력 값을 받아 가중합을 계산하고, 활성화 함수를 통해 출력을 계산합니다.
  3. 오차 계산: 출력 결과와 실제 값 사이의 차이를 계산합니다. 이는 오차(error)로, 퍼셉트론에서 단순히 출력값과 실제 값의 차이로 표현됩니다.

  4. 가중치 및 편향 업데이트: 오차를 기반으로 가중치와 편향을 업데이트합니다. 이때 퍼셉트론 학습 규칙은 다음과 같이 정의됩니다:

    $w_i \leftarrow w_i + \Delta w_i$ $\Delta w_i = \eta \cdot (y - \hat{y}) \cdot x_i$

    여기서 $\eta$는 학습률(learning rate), $y$는 실제 출력값, $\hat{y}$는 퍼셉트론의 예측값입니다. 학습률은 가중치 업데이트의 크기를 조절하는 중요한 하이퍼파라미터입니다. 오차가 크면 가중치가 더 크게 조정되고, 오차가 작으면 작은 범위로 조정됩니다.

  5. 반복: 이 과정을 여러 번 반복하여 가중치가 최적화되도록 합니다.

퍼셉트론의 수식

퍼셉트론을 수식으로 표현하면 아래와 같이 표현할 수 있습니다.

  1. 퍼셉트론의 가중합 (Weighted Sum):

    \[z = \sum_{i=1}^n w_i x_i + b\]

    여기서 $w_i$는 각 입력의 가중치, $x_i$는 입력값, $b$는 편향을 나타냅니다.

  2. 퍼셉트론의 출력:

    \[y = f(z) = f\left(\sum_{i=1}^n w_i x_i + b\right)\]

  3. 업데이트 규칙:

    \[w_i \leftarrow w_i + \Delta w_i\]

    여기서 $\Delta w_i$는 다음과 같이 계산됩니다:

    \[\Delta w_i = \eta (y - \hat{y}) x_i\]

    $\eta$는 학습률, $y$는 실제 출력값, $\hat{y}$는 퍼셉트론의 예측값입니다.

  4. 편향 업데이트 규칙:

    \[b \leftarrow b + \Delta b\]

    여기서 $\Delta b$는 다음과 같이 계산됩니다:

    \[\Delta b = \eta (y - \hat{y})\]

퍼셉트론의 한계

  1. 선형 분류 문제만 해결 가능: 퍼셉트론은 선형 분류기(Linear Classifier)이므로, 데이터가 선형적으로 구분될 수 있을 때만 문제를 해결할 수 있습니다. 즉, 직선 하나로 두 클래스를 나눌 수 있을 때만 효과적으로 동작합니다. 그러나 비선형 문제(XOR 문제 등)를 해결할 수 없습니다.

    예를 들어, XOR 문제는 아래와 같은 데이터셋으로 구성됩니다: * (0, 0) → 0 * (1, 1) → 0 * (0, 1) → 1 * (1, 0) → 1

    이 문제는 단일 퍼셉트론으로는 해결할 수 없으며, 이는 퍼셉트론의 중요한 한계 중 하나입니다.

  2. 활성화 함수의 제한: 기본 퍼셉트론에서는 계단 함수를 사용하여 이진 출력을 생성하지만, 이 함수는 미분이 불가능하여 역전파(backpropagation)를 사용할 수 없습니다. 다층 퍼셉트론에서는 이를 해결하기 위해 미분 가능한 활성화 함수(예: 시그모이드 함수, ReLU 등)를 사용합니다.

퍼셉트론의 역사적 의의

퍼셉트론은 단순한 구조에도 불구하고 인공지능과 머신러닝 분야에서 중요한 발전을 이루어낸 모델입니다. 특히, 퍼셉트론은 신경망의 개념을 도입하고, 학습을 통해 모델의 성능을 향상시킬 수 있는 아이디어를 제공했습니다. 그러나 퍼셉트론은 XOR 문제와 같은 비선형 분류 문제를 해결할 수 없다는 한계로 인해 이후의 연구에서는 다층 퍼셉트론과 같은 더 복잡한 신경망 구조가 개발되었습니다.

퍼셉트론의 발전은 딥러닝(Deep Learning)으로 이어졌으며, 이 과정에서 역전파 알고리즘의 도입과 활성화 함수의 다양화가 중요한 역할을 했습니다.

요약

  • 퍼셉트론은 입력 값의 가중합을 계산하고, 활성화 함수를 통해 이진 분류를 수행하는 단순한 신경망 모델입니다.
  • 입력 값에 가중치와 편향을 적용하여 계산한 가중합이 임계값을 넘으면 출력값으로 1을, 넘지 않으면 0을 반환하는 방식입니다.
  • 퍼셉트론은 선형 분류 문제만 해결할 수 있으며, XOR 문제와 같은 비선형 문제는 해결할 수 없는 한계가 있습니다.
  • 학습은 오차를 기반으로 가중치를 조정하는 방식으로 진행되며, 이 과정에서 학습률이 중요합니다.

참고문헌

  1. Rosenblatt, F. (1958). The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain. Psychological Review, 65(6), 386-408.
    • 퍼셉트론의 기본 개념을 처음 제안한 논문으로, 퍼셉트론의 구조와 작동 방식을 설명합니다. 이 논문은 신경망 연구의 기초를 마련한 중요한 연구입니다.
  2. Minsky, M., & Papert, S. (1969). Perceptrons: An Introduction to Computational Geometry. MIT Press.
    • 이 책은 퍼셉트론이 해결할 수 없는 문제, 특히 XOR 문제와 같은 비선형 문제에 대한 한계를 설명합니다. 이 연구는 퍼셉트론의 한계와 이를 극복하기 위한 다층 신경망 연구의 중요성을 부각시켰습니다.
  3. Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. Nature, 323, 533-536.
    • 퍼셉트론의 한계를 극복한 다층 퍼셉트론(Multilayer Perceptron, MLP)과 역전파 알고리즘을 설명한 논문으로, 딥러닝의 발전에 중요한 기여를 한 연구입니다.